Dr. Utr. Iur.
Frank
Van den Broeke

Minimalism

From the Ancient to Borromini
'Once Borromini has bitten you he never lets go." So, in 1948, Anthony Blunt, surveyor of the queens's pictures, advised Kerry Downes, a budding architectural historian who had recently gone up from Ealing Priory School to the Courtauld where Blunt was director. Downes had written Blunt a "dreadful, if enthusiastic" first essay on the work of Francesco Borromini, the 17th-century baroque architect. Although notoriously aloof, Blunt had spotted a spirited fellow enthusiast for the most exhilarating, if controversial, of all Roman architects – indeed of all architects of all eras – and Borromini had certainly got his teeth into Downes.
Without doubt, this architect is my favourite in the history. He knew the past, applied twists in it and brought it to the modern times. A genius, that only a few people managed to see, even at his time. What came after him, Gaudi, Wright Lloyd Frank, liberty, Art Nouveau, Jugendstill, are only variations on his ideas. I call him the “David Copperfield of Architecture” – The Magician. He was not born as an architect, but as a stonemason in the district of Ticeno (the Italian speaking part of Swiss, in those days belonged to the diocese of Milan, where was the former famous cardinal Carlo Borromeo). Was born the 25th September 1599, less than a year after his eternal rival Bernini (7th December 1598). They would die also almost at the same age. Borromini died on 3rd August 1667, Bernini 28th November 168o. It was said he change his name in Borromini after St. Charles Borromeo, from the diocese he came from.
Architectural Introduction
Minimalism
What makes for me Borromini the greatest architect? I would say his “Minimalism”. For sure, it’s a word that is in the mouth of every modern architect. But do they know what “minimalism” really is? I doubt. It took me a long time before finding a suitable definition. And finally for me, minimalism is the technique where you try to copy “nature”. Nature by definition is minimalist. “A minimum input of energy to achieve the maximum of a result”. And the only result that counts in nature is surviving, procreation. Whatever is not fulfilling that gets eliminated. Isn’t it incredible that everybody can make babies? It’s so easy … And who knows, maybe one of them will become Einstein! Or think about a simple egg. Can you break it pushing the shell from top to bottom? No! Do you know, if we could lift the St. Peter’s Basilica in Rome, putting under each of the four corners an egg, bringing it down, we would not break them! And the shell has only the thickness of one third of a fingernail: that is really minimalist. And in the egg is everything for procreation.
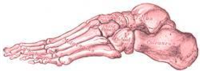
Give a look at the Coliseum in Rome; I would not call it minimalist by the size, being the biggest in his kind in the history, but it is minimalist by its structure thanks to one of the inventions of the Romans: The Arch: build in the shape of an egg, and all with arches. And is the “arch” not one of the strongest parts of our body? Look at the human foot: The tarsus forms a considerable part of the foot, and is placed at right angles to the leg, a position which is almost peculiar to man, and has relation to his erect posture. In order to allow of their supporting the weight of the body with the least expenditure of material the tarsus and a part of the metatarsus are constructed in a series of arches.
Probably the most famous arch we have in our body is the aortic arch, something that has to work from the moment of the conception until our dead, and is not allowed to break.
And now, go in the Coliseum, and look around: wherever you’re eye is going, you will see arches. What a building. Arches, the shape of an egg ………. !
The strongest construction in the world. As we know, on the to top of the arch is sitting the “keystone”. The shape of this stone makes that it never can fall down, but when there is coming an earthquake, it will push a little bit more to the left and to the right. And than you build your coliseum like an egg: the more earthquakes you have, the more the building get settled. I still wonder why, in countries with frequent earthquakes, they don’t build for the poor people house in the shape of an egg and with arches? If there is an earthquake, maybe the windows will blow out, but at least the structure will hold and you will survive. The only reason that I can imagine is that it is difficult to find an engineer or architect who is making money with empty walls … and that is an arch. But copying nature it does everything to survive.
As we see later, something Borromini would know it and use it up to its perfection.

The concept “One”
Much ado about nothing! The number zero as we know it arrived in the West circa 1200, most famously delivered by Italian mathematician Fibonacci (aka Leonardo of Pisa), who brought it, along with the rest of the Arabic numerals, back from his travels to north Africa. But the history of zero, both as a concept and a number, stretches far deeper into history—so deep, in fact, that its provenance is difficult to nail down. We have to thank the Muslims, because they invented nothing. It looks like a line for creating war: but nothing lesser than that: they really invented “nothing”, the number zero. Can you imagine yourself without the concept “zero”? Forget computers (binary system), electricity and so on. Robert Kaplan, author of The Nothing That Is: A Natural History of Zero (Oxford University Press, 2000) says: “It began to take shape as a number, rather than a punctuation mark between numbers, in India in the fifth century A.D.”. I was told, it was an Iranian woman who invented it, but being Muslim, she couldn’t claim it; so, her husband the doctor did it. The second appearance of zero occurred independently in the New World, in Mayan culture, likely in the first few centuries A.D. "That, I suppose, is the most striking example of the zero being devised wholly from scratch," Kaplan says.
But, we Europeans had no clue of the Mayan culture. The Romans knew only the philosophy of Zeno, the leader of the stoicisms. Zeno, in the beginning, as the rest of his Sophist colleagues, were obsessed with the idea that motion was not logically possible. The sophists considered that motion was only possible through emptiness. But empty was not possible logically. Only what exists, was the central idea of their philosophy. What does not exist does not exist; therefore there is no emptiness or nothingness; therefore the motion is not possible. The false reasoning persisted after Socrates, indeed to our day. Even a great mind such as Aristotle strongly affirmed that motion was not possible from a logical standpoint! The solution needed such a long time … for it's all about Time! Zenon made an extremely attractive art to prove that motion was not possible. He came up with a riddle that used Achilles as the main character. We know that the legendary hero was also known as the Quick-Foot Achilles, or Speedy Achilles. Really? Zeno questioned the speed of Achilles. I, Zeno, will prove that your speedy Achilles will never beat a tortoise in a running race!

Okay, your Achilles is faster than a tortoise, admitted Zeno. Therefore we must necessarily give the tortoise a long start. But here is the kicker, puzzled Zeno his audience. Achilles does reach the starting point of the tortoise. But when Achilles reaches that space, the tortoise would reach a farther position in space. Let's name it position 2. When Achilles reaches position 2, the tortoise would have reached a new position; let's name it position 3. When Achilles reaches position 3, the tortoise would have reached a new position; let's name it position 4. When Achilles reaches position 4, the tortoise would have reached a new position; let's name it position 5. And so on ad infinitum. Achilles can never pass the tortoise...
Many thinkers have been impressed by that logical construct. We are talking here over two thousand years and millions of admirers of a paradox! Is it really a paradox? Is it really an impeccably logical argument that leads to a false conclusion? Not! Non!
The argument is NOT logical. Logic assumes that ALL the elements of a system are present. Leaving out just one element makes the system not only ILLOGICAL, but also, worse, ABSURD. Absurdity is the opposite of logic.
Motion assumes two and exactly two elements: Space and Time. Motion is represented relationally by Speed. Speed equals Space over Time (v = s / t). Zeno eliminates one of the sine-qua-non elements: Time. Zeno equation of Speed (or velocity, hence v) leads to the absurdity: v = s / s. Metaphorically speaking; Zenon amputates one of Achilles' legs! Amputate one of anybody's legs — and the person would fall down motionless! It is not a paradox!
Zeno's paradox takes into account Space only. Time is completely ignored. Achilles will cover one unit of space in less time than the tortoise. Equivalently, Achilles will cover a longer distance than the tortoise in the same time. By the time Achilles reaches the starting point of the tortoise, the tortoise would have moved a shorter distance. The distance could be so short that Achilles could surpass it in a very short time. Generalizing, the gap gets shorter and shorter as the time progresses. At some point in time — NOT point in space — the gap reverses. The faster competitor surpasses the slower competitor who had an early start.
It's a no-brainer! It all depends on the speeds of the two competitors. At equal speeds, the competitor with an early start will be always in front, keeping the same gap between her and the competition. It is not the case here. Zeno admits that Achilles is faster than the tortoise. Let's say Achilles is 10 times faster (in reality, a human is much faster than that compared to a tortoise). Let's say the tortoise has a ten-meter early start. The tortoise is 10 meters ahead of Achilles. Achilles walks, instead of running. He walks ten meters in ten seconds. When Achilles reaches the starting point of the tortoise, the Sophist's favourite will be exactly one meter ahead. It took 10 seconds to reach the new point in space. In the next 10 seconds, Achilles will be 8 meters ahead of the tortoise. The tortoise is no longer ahead. Motion does not stop at so-called “points in space”. Motion is fluid in Space AND Time.
There is a similar Zeno riddle: The arrow and the bow paradox. Zeno had to create this new one because he realized the fundamental flaw of Achilles and the tortoise. Probably many contemporaries posed Zeno with the inherent absurdity of his riddle. Zenon himself admits that Achilles is faster than the tortoise. Therefore, the tortoise must be placed ahead of Achilles. By admitting that an element is faster than the other, the implication of motion is mandatory!
The arrow will never leave the bow, because it must surpass first half the distance between the bow and the target, reckons Zenon of Elea. Before that, the arrow must surpass half of the half the distance. Further backwards, half of the half of the distance; and so on ad infinitum.
Roman Architecture
For Zeno, everything can be reduced to the half of the half ad infinitum. You never reach “nothing”. But his ideas influenced the whole of roman and Greek architecture. They didn’t know what nothing was! But from where you start building your house, if you can’t start from nothing? Than, of course you have to start from “One”; and that made the magnificent architecture of the renaissance. And renaissance was intrinsic copying the Roman and the Greek.
If you look at the frescoes, token from the house of the emperor Augustus on the Palatine hill in Rome, you will see a Tuscany City. And aren’t they beautiful? So different from some modern architecture, where every house has the same size. In the Victorian England, they painted the doors in those beautiful different colours (the national trust colors of England: Farrow and Ball – I used them in my own house: the best of the best), so that at least, drunk people would enter the right door by night. That problem didn’t exist in the Roman time. Every house had a different height.
If I was a wealthy tourist, and approaching a city like today’s Florence in the renaissance, viewing it from the top, I would know immediately which house I would try to be invited for supper: he highest one.
And it had all to do by the fact that the renaissance builders didn’t use the concept zero!
How you build the perfect house?
You start from “one”, because “zero” doesn’t exists. And that means you’re copying nature. Even Nature doesn’t know what nothing is. Today, in Genève-Swiss, in CERN, they try to recreate the big ban. And the whole process is about the first cell. You need ONE cell for making two, and two for making four. But from where is coming the first one? That’s the Big Bang. The beginning of life. The Romans, who started there counting with ONE, (after the half of the half of the half.. something is still left: one!) made their architecture similar to nature, that starts also with ONE. Do you know, if you take a rope and turn it around your thumb, twice your thumb is your wrist, twice your wrist is you neck, twice your neck is your waist, but that can change during lifetime! That’s nature: takes one and double it. And again, we find that in the human body: the size of your foot multiplied will be the size of your body. Your foot has also the same size of the bone in your arm.
It’s also the Vetruviun man of Leonardo da Vinci:
counting the human body from top to bottom is exactly the same distance between his two spreaded arms. 1 = 1. The square shows you. And Vitruvius was the most renowned architect of Julius Caesar. It’s not for nothing they put it on the back of the 1,00 € coin in Italy. An interesting book: Vitruvius: Ten books on architecture. Marcus Vitruvius Pollio was born approx 80 BC and was Caesar's architect for design, architecture and construction of artillery machines. His fame dispappeared in obscurity during the Medieval but reemerged during the renaissance by the italian humanist Poggio Bracciolini, who also rediscoverd Cicero's orations and Lucretius poem On the Nature of Things.
Brunelleschi used it as an inspiration when he came to Rome to study the ruins of classical buildings, and Alberti quoted it often in his treatise on Architecture. Toward the end of the 15th Century, Leonardo da Vinci wrote in a notebook "Enquire at the stationers about Vitruvius". It was what a renaissance man tried to achieve: the relationship between the microcosmos of man and the macrocosmos of the earth. (Walter Isaacson: The inspiration behind Leonardo da Vinci's Vetruvian Man)
So, Let say, are rich, you have a plot of land and you want to build a house. You take a rope, the size of the plot and you divide it in two, four, eight …. Finally you have the place to put your first column. And so, the second …. What we see on our left is the Chiostro del Bramante, build by the one of the most famous architects of the renaissance: Bramante. It could be the courtyard of a Roman villa. (If you are in Rome, walk in and have a drink or cheap lunch in the “Cafeteria” on the first (USA)/ second floor (Europe) of the Chiostro del Bramante and there is the One again:
We Europeans speak about the second floor, when Americans are speaking about the first floor. They don’t know what Zero is. Or you live in the basement (-1 in Europe) or 1 (ground floor in Europe) or in 2nd (1st floor in Europe). The reason the Americans still think in that way was that they where discovered in 1492 by Vespuccio Amerigo and Christopher Columbus, in the middle of the Renaissance time, copying the roman and the Greek. And therefore they are starting with One. And in this building, the Chiostro del Bramante, the one is the unit from the middle of one column to the middle of the next one; the same unit is used for going up by multiplying it. Do you need a door? It’s the half of the unit. You need a text above the door? The halve of the halve of the halve for making the size of your letters will do it. Even in in the way Americans are writing their numbers: for the number one, they use the latin form (I), while in europe the use the Arab symbol (1).
It’s only after 9/11 that Americans started to speak about “ground Zero”, because in the blast, even One was destroyed.
And therefore, approaching a Renaissance city from above, like Florence, I’m looking for the highest house: that’s the one with the biggest plot of land, and his ONE is greater in all directions. And therefore he is the wealthiest of all: there I have to go to a party, nowhere else.
Using the One is the first rule; the second is the Fibonacci sequence or the golden ratio.



The Sequence of Fibonacci
Beware! Here is some maths involved, but I will try to make it easy, let’s talk about rabbits …
He was called the "greatest European mathematician of the middle ages", and his full name was Leonardo of Pisa, or Leonardo Pisano in Italian since he was born in Pisa, Italy, the city with the famous Leaning Tower, about 1175 AD. Pisa was an important commercial town in its day and had links with many Mediterranean ports. Fibonacci’s father, Guglielmo Bonacci, was a kind of customs officer in the present-day Algerian town of Béjaïa, formerly known as Bugia or Bougie, where wax candles were exported to France. They are still called "bougies" in French. He grew up with a North African education under the Moors and later travelled extensively around the Mediterranean coast. He would have met with many merchants and learned of their systems of doing arithmetic. He soon realised the many advantages of the "Hindu-Arabic" system over all the others and especially over the Roman numbers (I, II….X, L, C, M….) it was almost impossible to calculate. With the Arabic numbers (0, 1, 2, 3 …) it became easy.
In the West, the Fibonacci sequence first appears in the book Liber Abaci (1202). Fibonacci considers the growth of an idealized (biologically unrealistic) rabbit population, assuming that: a newly born pair of rabbits, one male, one female, are put in a field; rabbits are able to mate at the age of one month so that at the end of its second month a female can produce another pair of rabbits; rabbits never die and a mating pair always produces one new pair (one male, one female) every month from the second month on. The puzzle that Fibonacci posed was: how many pairs will there be in one year?
ß
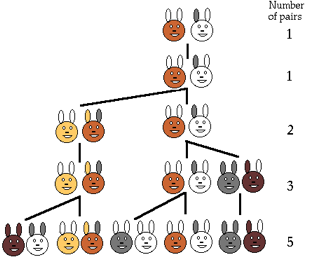
At the end of the first month, they mate, but there is still only 1 pair.
•At the end of the second month the female produces a new pair, so now there are 2 pairs of rabbits in the field.
•At the end of the third month, the original female produces a second pair, making 3 pairs in all in the field.
•At the end of the fourth month, the original female has produced yet another new pair, the female born two months ago produces her first pair also, making 5 pairs.
That inspired him to make his sequence:
1- 1- 2- 3- 5- 8- 13- 21- 34- 55- 89- 144- 233- 377- 610- 987- 1597- 2584- 4181- 6765…. You just ad the previous number with the next one, and so on: (1+1=2); (1+2=3); (2+3=5) …. And so on.
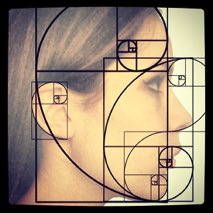
Now is the question what has that to do with architecture? Very simple: let’s take the last number: 6765 and you divide it by the former number: 4181. The result will be: 1,61803396…. Whenever you will divide a number of the sequence by the former number you will have approx the same result. It is an infinite number, just like , pi, but this one is called , the Greek letter Phi.
And now we can start to make the perfect temple.
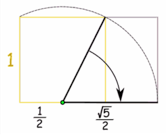
Here is one way to draw from a square a rectangle with the Golden Ratio:
•Draw a square (of size "1")
•Place a dot half way along one side
•Draw a line from that point to an opposite corner (it will be √5/2 in length)
•Turn that line so that it runs along the square's side
•Then you can extend the square to be a rectangle with the Golden Ratio. And that is the sequence of Fibonacci: multiplying the 1 with , 1,618…. We are creating the rectangle. Inside the rectangle, we can design an other square, and making another golden ratio. And we are making our own temple like the Partheon on the Acropolis in Greece.
Simple, isn’t it?

But the amazing thing is that, while you are looking at architecture, in fact you are looking at Nature. Because it is exactly the distance from your bellybutton to your feet, multiplied by 1,61803… and you arrive at your head. Again the Vetruvian man of Leonardo da Vinci
. But further, put your thumb against your first finger (from square making a rectangle), what’s over is the size of your nose, from your chin to your nose, from your nose to your brains, from your nose to your ears etc.
It is always the golden rectangle. It is everywhere in nature. Look at the pictures below. Or try it by yourself and click: Golden Ratio in Nature: There is the sunflower, the Nautilus-shell, leaves of trees and so much more. Al those techniques were used by architects like Borromini, Gaudi and all the minimalists.
If you want to learn more about it, connect yourself with the following hyperlink. It will conduct you to a website where they are trying to explain it to children. Go to it and try it out: The golden ratio for children.

Let’s go now to Borromini
Have a look at his buildings! There is written an excellent book about Borromini, by Anthony Blunt (I mentioned him earlier with a quote from him in the beginning) and for sure, Anthony Blunt was a colorful figure. The memoirs of Anthony Blunt, the so-called Fourth Man in the Cambridge Five spy ring, are made public for the first time in 2009, twenty-five years after his dead. Anthony Blunt, once a trusted art adviser to George VI and the Queen Elisabeth II, betrayed his country because of his fascination for the young Cambridge undergraduate Guy Burgess. He was knighted in 1956, but under Margaret Thatcher he was exposed in Parliament as a traitor, stripped of his knighthood, and to contemplate suicide because of the public disgrace. Probably he was one of the most notorious double-spies in the history. They say that Ian Fleming inspired himself on this gentleman for creating his character of James Bond. Being the art adviser of Betty, the Queen, allowed him to travel all the world. Becoming a double-spy used up his free time. In my articles about Ancient Rome, I will say a bit more about his spy-business. But his work on Borromini is still remarkable. I think that the book description in Amazon.com is excellent: “Borromini is one of the great geniuses of Baroque architecture, perhaps the greatest in inventiveness and in use of spatial effects. (Not for nothing I call him the David Copperfield of Architecture, the magician !) Here is the first book in English to survey the whole work of the master. The author, former Director of the Courtauld Institute of Art, is known internationally for his many works on French and Italian architecture and painting. In this lucid and fully illustrated account Anthony Blunt charts Borromini's career and analyzes and assesses his art. Mr. Blunt tells of Borromini's training, relating his style to that of Bernini, under whom he worked, and to the architecture from which he learned, for example Michelangelo's. Borromini's patrons allowed him freedom to evolve his own ideas, and his originality and imagination in inventing new architectural forms become apparent as the author studies individual commissions. His imagination was apparently limitless, but his inventions evolved in terms of rigidly controlled geometry. It is this combination of revolutionary inventiveness and intellectual control that gives Borromini's work particular appeal in the twentieth century.”
But the whole was inspired on the past, applying to the new. Borromini can inspire modern minimalism. I would like to discover with you some of his most amazing buildings: San Carlino alle quattre Fontane, Sant’Ivo alla Sapienza, the Oratory, Spada’s house, the chapel in palazzo Doria-Pamphilij, St. John in Lateran… just to mention a few.
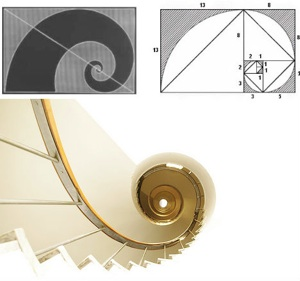



When it comes to material design or architecture, Mother Nature has something of an advantage over modern sience. After all, Her research and development cycle is measured in million of years.
Look at the video below to discover where we can find the Golden Ratio